선택도(Selectivity)
PostgreSQL의 옵티마이저는 쿼리 성능을 최적화하기 위해 FROM, WHERE, JOIN과 같은 다양한 조건절의 선택도(selectivity)를 추정한다. 선택도를 추정한다는 의미는 전체 레코드 수에서 조건을 만족하는 레코드 수의 비율이 얼마나 되는지를 추정한다는 의미이다. 선택도 값에 따라 옵티마이저는 테이블을 스캔할지, 인덱스를 사용할지, 어떤 조인 순서를 택할지 등 가장 효율적인 실행 계획을 결정한다.
수학적으로는 다음과 같이 표현된다.
- 선택도 (S) = 예상 결과 행 수(
sᵢ) / 전체 튜플 수(nᵢ)
(선택도(S)는 쿼리 조건𝝷를 만족하는 튜플이 릴레이션에 나타날 확률이며, 이는 예상 결과 행 수를sᵢ, 전체 튜플 수를nᵢ라고 할 때sᵢ / nᵢ로 정의된다)
즉 레코드 1개가 WHERE절 조건을 만족할 확률이라고 볼 수 있다. 쿼리 실행 계획 선택, 조인 순서 결정((A ⋈ B) ⋈ C 또는 A ⋈ (B ⋈ C)), 해시 테이블 크기 계산, 병렬 처리 등 다양한 내부 처리에서 선택도를 활용한다. 따라서 선택도가 얼마나 정확히 추정되느냐에 따라 쿼리의 성능이 크게 달라질 수 있다.
다행히 대부분의 OLTP 서비스 쿼리(OLTP 환경으로 단정지었지만)는 단일 테이블을 기준으로 동등 조건(=), 비교 조건(>=, <=), 논리곱(AND), 논리합(OR) 등을 단순하게 사용하는 경우가 많기 때문에, 선택도 계산 방식이나 통계 활용 방식도 비교적 단순한 편이다.
이번 내용에서는 몇 가지 예제를 중심으로 선택도가 실제로 어떻게 계산되는지, PostgreSQL은 어떤 통계를 바탕으로 선택도를 추정하는지, 그 과정을 살펴보도록 하겠다.
통계와 샘플링
PostgreSQL의 통계는 크게 기본 통계와 확장 통계로 나눌 수 있다. 기본 통계는 확장 통계를 사용하지 않을 경우 기본으로 사용되는 통계이며, 확장 통계는 기본 통계가 가진 문제를 보완하기 위해 나중에 추가된 통계이다. 필요에 의해 확장 통계를 생성한 경우를 제외하고는 일반적으로 기본 통계가 사용된다.
| 기본 통계 | 확장 통계 |
|---|---|
| MCV (Single Field) | MCV (Multi Fields) |
| Histogram | Dependencies |
| Correlation | N-Distinct |
| …(생략) | …(생략) |
<표 1>을 보면 기본 통계인지 확장 통계인지에 따라 지원되는 통계 종류들을 확인할 수 있는데, 이 통계들은 WHERE절 조건에 따라서 적절히 조합된 형태로 사용된다. 통계 계산은 샘플링된 통계 데이터를 기반으로 동작하며, 샘플링의 기준은 300 * default_statistics_target 으로 고정되어 있다. default_statistics_target 파라미터는 100이 기본 값이기 때문에 샘플링은 30,000개의 행을 대상으로 한다. 샘플을 수집할 때는 내부적으로 Reservoir Sampling 이라는 알고리즘을 사용하는데, 통계 데이터 전체를 메모리에 저장할 수 없어서 랜덤 샘플을 메모리 효율적으로 수집하기 위해 해당 알고리즘이 사용되었다고 보면 된다. 그리고 샘플링 30,000개라는 기준은 “Random sampling for histogram construction: how much is enough?” 라는 제목의 논문에서 기인했는데, 이 논문에서 정의한 공식을 1,000,000행 정도의 현실적인 값으로 대입하면 약 30,000 정도의 수치가 나온다.
그럼 여기서 1,000,000행은 어떤 기준인지에 대한 물음이 생기는데, 이에 대한 답변은 아래 계산 과정을 참고해보면 좋다. 𝑛이 증가하는 것 대비 로그 값의 변화가 크지 않기 때문에(100만개 행 -> 19.1, 1억개 행 -> 24.1, 1조개 행 -> 28.5) 현실적으로 정해진 수치라고 생각하면 된다.
계산 과정
=> 샘플 수 𝓇 = 4 ᐧ 𝑘 ᐧ ln(2𝑛/𝛾)/𝑓²
- 𝑘 = default_statistics_target
- 𝑓 = 허용 오차 (𝑓 = 0.5이면 bin 크기 ±50%까지 허용)
- 𝛾 = 오차 초과 확률 (1% 오류 확률은 𝛾 = 0.01)
현실적인 값으로 계산 시,
- ln(2𝑛/𝛾) ≈ 19.1 (n=1,000,000, γ = 0.01)
- 𝑓 = 0.5 이므로 𝑓² = 0.25
- 𝓇 ≈ 4 ᐧ 𝑘 ᐧ 19.1/0.25 ≈ 305.6 ᐧ 𝑘
𝑘는 100이므로,
=> 𝓇 ≑ 30,000
통계 수집 항목
자동(auto)이든 수동(manual)이든 PostgreSQL 서버에서 ANALYZE(VACUUM ANALYZE, VACUUM FULL, CREATE INDEX, CLUSTER 포함) 명령을 수행하면 PostgreSQL 백엔드 프로세스가 해당 명령을 받아 샘플링을 수행하고, 통계 정보를 수집한다. 테이블 통계 수집은 테이블의 전체 크기, 행 수 등 물리적인 저장 특성과 관련된 정보들을 수집하지만, 컬럼 통계 수집은 컬럼 타입의 특성에 따라서 각기 다른 수준의 통계를 수집한다.
컬럼 타입의 특성에 따라서라는 말은 컬럼 타입마다 지원하는 연산자(operator)가 다르다는 것인데, 여기서 말하는 연산자는 equal(=)과 less than(<) 연산자를 의미한다. 연산자의 종류는 많지만 통계 수집 항목을 결정하는 연산자는 equal(=)과 less than(<) 2개가 사용된다.
두 연산자를 모두 지원하는 컬럼 타입이면 <표 2>에서와 같이 Scalar 통계를 수집하며, equal 연산자만 지원하는 컬럼 타입이면 Distinct 통계를 수집한다. 그리고 지원하는 연산자가 없는 경우에는 Trivial 통계를 수집한다. 아마 위에서 설명한 기본 통계 및 확장 통계와의 관계성이 궁금할 수도 있는데, 관계성은 아래와 같은 계층구조로 생각해볼 수 있다. 기본 통계와 확장 통계는 물리적으로 저장되는 카탈로그 자체가 다른 것이고, Scalar, Distinct, Trivial 통계 수준은 기본 통계 범주안에서 논리적으로 나뉘어진 개념인 것이다.
├── 기본 통계 (pg_statistic 기반, 단일 컬럼 단위)
│ ├── Scalar 수준
│ ├── Distinct 수준
│ └── Trivial 수준
└── 확장 통계 (pg_statistic_ext 기반, 다중 컬럼 또는 이외 확장 통계)
├── ndistinct
├── dependencies
└── MCV (multivariate)
연산자 이야기로 돌아와서, 통계 수준을 결정하는 조건에 특정 연산자(=, <)만 사용하는 이유는, 동등 비교가 가능한지, 순서 비교가 가능한지만 판단하면 되기 때문이다. greater than(>) 연산자는 less then(<) 연산자와 교환법칙으로 대응이 가능하며, greater than or equal to(>=), less then or equal to(<=) 연산자는 equal(=), less than(<) 두 연산자의 조합으로 대응이 가능하다.
* a >= b는 NOT (a < b) AND (a = b), a <= b는 (a < b) AND (a = b)로 독립 처리
| Scalar 통계 | Distinct 통계 | Trivial 통계 |
|---|---|---|
| INTEGER NUMERIC TEXT VARCHAR JSONB TIMESTAMP DATE BYTEA INET CIDR … …(생략) | CID ACLITEM … …(이외 동등 연산자만 정의한 커스텀 타입 등) | JSON POLYGON POINT … …(이외 연산자가 정의되지 않은 사용자 정의 타입 등) |
각 통계 수준에서 지원하는 통계 수집 항목은 <표 3>과 같다. null_frac(null 비율), avg_width(null을 제외한 평균 바이트 크기), n_distinct(null을 제외한 컬럼의 고유한 값의 수)는 통계 수준에 관계없이 기본적으로 수집되는 항목임을 확인할 수 있다. 히스토그램은 MCV에 포함되지 않는 고유값이 2개 이상인 경우(최소 1개 이상의 구간)에만 생성되는 통계 항목이기 때문에 Scalar 통계 수준에 포함된다고 해서 무조건적으로 생성되지는 않는다.
* 히스토그램은 경계값(boundary)의 배열로 저장된다. 경계값이 N개라면, 히스토그램 구간은 N-1개이다.
| Scalar 통계 | Distinct 통계 | Trivial 통계 |
|---|---|---|
| null_frac | null_frac | null_frac |
| avg_width | avg_width | avg_width |
| n_distinct | n_distinct | n_distinct(unknown) |
| MCV | MCV | (수집 안함) |
| Histogram | (수집 안함) | (수집 안함) |
| Correlation | (수집 안함) | (수집 안함) |
여기서 잠시 JSON 타입의 경우를 생각해보자. 수십 개의 키 값이 중첩되어 있는 JSON 데이터는 어떤 기준으로 정렬해야 할지에 대한 고민이 생긴다. JSON 타입 자체로는 기준이 없기 때문에 순서 비교가 불가능하다. 하지만 JSON 타입의 함수 기반 인덱스는 함수의 반환 값을 기준으로 정렬하기 때문에 순서 비교가 가능하다. 예를 들어 fx_name(info ‒>>’name’::text) 이라는 이름의 함수 기반 인덱스는 반환 값이 text이기 때문에 Scalar 통계 수준에서 각 통계 항목을 수집할 수 있다.
컬럼 타입의 특성에 맞게 수집된 통계 데이터는 pg_statistic 이라는 시스템 카탈로그에 저장된다. 테이블의 스키마를 보면 stakind1 부터 stavalues5 컬럼까지 suffix의 숫자를 달리한채 동일한 컬럼명이 반복되는 것을 확인할 수 있는데, 이는 컬럼 타입당 최대 5개까지의 통계 항목을 저장할 수 있기 때문이다.
╔═════════════╦══════════╦═══════════╦══════════╦══════════════╦═════════════╗
║ Column ║ Type ║ Modifiers ║ Storage ║ Stats target ║ Description ║
╠═════════════╬══════════╬═══════════╬══════════╬══════════════╬═════════════╣
║ starelid ║ oid ║ not null ║ plain ║ null ║ null ║
║ staattnum ║ smallint ║ not null ║ plain ║ null ║ null ║
║ stainherit ║ boolean ║ not null ║ plain ║ null ║ null ║
║ stanullfrac ║ real ║ not null ║ plain ║ null ║ null ║
║ stawidth ║ integer ║ not null ║ plain ║ null ║ null ║
║ stadistinct ║ real ║ not null ║ plain ║ null ║ null ║
║ stakind1 ║ smallint ║ not null ║ plain ║ null ║ null ║
║ stakind2 ║ smallint ║ not null ║ plain ║ null ║ null ║
║ stakind3 ║ smallint ║ not null ║ plain ║ null ║ null ║
║ stakind4 ║ smallint ║ not null ║ plain ║ null ║ null ║
║ stakind5 ║ smallint ║ not null ║ plain ║ null ║ null ║
...
...
...
║ stavalues1 ║ anyarray ║ ║ extended ║ null ║ null ║
║ stavalues2 ║ anyarray ║ ║ extended ║ null ║ null ║
║ stavalues3 ║ anyarray ║ ║ extended ║ null ║ null ║
║ stavalues4 ║ anyarray ║ ║ extended ║ null ║ null ║
║ stavalues5 ║ anyarray ║ ║ extended ║ null ║ null ║
╚═════════════╩══════════╩═══════════╩══════════╩══════════════╩═════════════╝
<표 3>의 MCV, Histogram, Correlation 통계 항목은 아래와 같이 내부적으로 고정적인 번호가 할당되어 있다. 이 중 4번과 5번은 표에 따로 언급되어 있지 않은데, 4번의 경우 복수 요소(elements)를 가진 타입의 컬럼(array, tsvector, jsonb[], text[], int[])에서 자주 나타나는 요소에 대한 통계이고, 5번의 경우는 고유 요소 개수의 분포를 히스토그램으로 나타낸 통계이다.
* 아래 6번과 7번에 해당하는 통계 항목(range 타입)까지 포함하면 내부에 할당된 번호는 7개이지만, 이번 내용에서는 다루지 않으므로 5개의 통계 항목을 지원한다고 가정한다.
– #define STATISTIC_KIND_RANGE_LENGTH_HISTOGRAM 6
– #define STATISTIC_KIND_BOUNDS_HISTOGRAM 7
// #define STATISTIC_KIND_MCV 1
- MCV: 1
// #define STATISTIC_KIND_HISTOGRAM 2
- Histogram: 2
// #define STATISTIC_KIND_CORRELATION 3
- Correlation: 3
// #define STATISTIC_KIND_MCELEM 4
- MCE(Most Common Elements): 4
// #define STATISTIC_KIND_DECHIST 5
- DECH(Distinct Elements Count Histogram): 5
예를 들어, 4번의 경우 아래 test4 테이블의 tags(text[]) 컬럼은 자주 나타나는 요소인 {db,index,jsonb,plan,postgres,sql,tsvector}에 대한 통계 데이터가 수집된다.
select * from test4;
╔════╦═══════════════════════════════════╗
║ id ║ tags ║
╠════╬═══════════════════════════════════╣
║ 1 ║ ['postgres', 'sql', 'db'] ║
║ 2 ║ ['sql', 'index', 'plan'] ║
║ 3 ║ ['postgres', 'jsonb', 'index'] ║
║ 4 ║ ['db', 'index', 'sql'] ║
║ 5 ║ ['postgres', 'tsvector', 'jsonb'] ║
║ 6 ║ ['sql', 'postgres', 'jsonb'] ║
║ 7 ║ ['jsonb', 'sql'] ║
║ 8 ║ ['index', 'plan'] ║
║ 9 ║ ['sql'] ║
║ 10 ║ ['postgres'] ║
║ 11 ║ ['jsonb', 'jsonb', 'sql'] ║
╚════╩═══════════════════════════════════╝
-- 수집된 통계 데이터
SELECT c.relname, a.attname,
s.stakind3, s.stavalues3, s.stanumbers3,s.staop3,s.stacoll3
FROM pg_statistic s
JOIN pg_class c ON s.starelid = c.oid
JOIN pg_attribute a ON s.staattnum = a.attnum AND a.attrelid = c.oid
WHERE stakind3 = 4
AND c.relname = 'test4'
-[ RECORD 1 ]-------------------------
relname | test4
attname | tags
stakind3 | 4
stavalues3 | {db,index,jsonb,plan,postgres,sql,tsvector}
stanumbers3 | [0.18181819, 0.36363637, 0.45454547, 0.18181819, 0.45454547, 0.6363636, 0.09090909, 0.09090909, 0.6363636, 0.0]
staop3 | 98
stacoll3 | 100
이렇게 5개의 통계 항목(MCV, Histogram, Correlation, MCE, DECH)은 stakind1 부터 stakind5 까지 수집 시기에 따라 순서대로 저장된다. 통계 항목은 보통 2~3개 정도 수집되기 때문에 실제 서비스에 사용되는 데이터는 대부분 stakind4, 5 필드가 비워져있다.
사실 통계를 좀 더 읽기 쉬운 형태로 제공하는 pg_stats 뷰가 있기 때문에 pg_statistic 테이블을 직접적으로 조회하는 경우는 거의 없다. 때문에 앞으로 나올 예제에서는 pg_stats 뷰를 사용한다.
이제까지 이야기한 내용을 간단하게 정리해보면 다음과 같다.
- 선택도(selectivity)는 “레코드 1개가 WHERE절 조건을 만족할 확률” 이며, 선택도에 따라 쿼리의 성능이 크게 달라질 수 있다.
- 통계 계산을 위한 샘플링은 300 * default_statistics_target이며, 기본적으로 테이블당 30,000개이다.
- 통계 수집 항목은 컬럼 타입이 지원하는 연산자에 따라 3가지의 통계 수준(Scalar, Distinct, Trivial)으로 나뉘어지며, 수집된 통계 데이터는 pg_statistic 카탈로그 테이블에 저장된다.
동등(Equal) 조건의 쿼리
동등 단일 조건
아래 employee 테이블에는 10,000명의 회사 직원 정보가 저장되어 있다.
동등(=) 단일 조건으로 테이블을 조회할 때는 선택도를 계산하는 방법이 아주 쉽다. pg_stats 뷰의 most_common_vals 값이 WHERE절의 조건 값이 되고, most_common_freqs 값이 해당 조건 값(Marketer)의 선택도가 된다. 즉 job=’Marketer’ 조건의 선택도는 8.78%이다. 10,000행의 8.78%는 878행으로, 옵티마이저의 실행 계획과 일치하는 것을 확인할 수 있다.
-- 동등(=) 단일 조건 쿼리
SELECT * FROM employee WHERE job = 'Marketer'
most_common_vals | {CustomerService,Marketer,Admin,HR,Developer,Production,Researcher,Designer,Logistics,Sales,Finance,Planning}
most_common_freqs | [0.0883, 0.0878, 0.085, 0.085, 0.084, 0.084, 0.0825, 0.0818, 0.0815, 0.0814, 0.0808, 0.0779]
-- 쿼리 실행 계획
EXPLAIN SELECT * FROM employee WHERE job = 'Marketer'
╔═════════════════════════════════════════════════════════════╗
║ QUERY PLAN ║
╠═════════════════════════════════════════════════════════════╣
║ Seq Scan on employee (cost=0.00..251.00 rows=878 width=66) ║
║ Filter: ((job)::text = 'Marketer'::text) ║
╚═════════════════════════════════════════════════════════════╝
동등 복합 조건
이번에는 2개 이상의 동등(=) 복합 조건이다. 동등 복합 조건은 확률에서의 논리곱(A ∩ B)과 같이 사건 A와 사건 B가 모두 일어나는 경우를 의미하기 때문에 2개의 사건을 독립적인 사건으로 가정한다. 즉 job = ‘Marketer’ AND region = ‘Jeju” 조건은 각각의 조건을 만족하는 튜플의 확률을 곱한 것과 같다. job = ‘Marketer’ 조건의 선택도는 8.78%, job = ‘Jeju‘ 조건의 선택도는 9.74% 이므로, 두 확률을 곱하면 0.0878 * 0.0974 = 0.00855172 ≑ 0.86% 이다. 10,000행의 0.86%는 86행(85.5 반올림)으로, 옵티마이저의 실행 계획과 일치하는 것을 확인할 수 있다. 이런식으로 논리곱이 N개 증가하면 N개 조건에 대한 선택도를 전부 곱하여 행 수를 추정할 수 있다.
-- 동등(=) 복합 조건 쿼리
SELECT * FROM employee WHERE job = 'Marketer' AND region = 'Jeju'
most_common_vals | {Busan,Chungcheong,Gwangju,Gangwon,Daejeon,Gyeonggi,Daegu,Jeju,Incheon,Seoul}
most_common_freqs | [0.1053, 0.1053, 0.1016, 0.1008, 0.1001, 0.0989, 0.098, 0.0974, 0.0968, 0.0958]
most_common_vals | {CustomerService,Marketer,Admin,HR,Developer,Production,Researcher,Designer,Logistics,Sales,Finance,Planning}
most_common_freqs | [0.0883, 0.0878, 0.085, 0.085, 0.084, 0.084, 0.0825, 0.0818, 0.0815, 0.0814, 0.0808, 0.0779]
-- 실행 계획
EXPLAIN SELECT * FROM employee WHERE job='Marketer' AND region='Jeju'
╔══════════════════════════════════════════════════════════════════════════════════╗
║ QUERY PLAN ║
╠══════════════════════════════════════════════════════════════════════════════════╣
║ Seq Scan on employee (cost=0.00..289.00 rows=86 width=66) ║
║ Filter: (((job)::text = 'Marketer'::text) AND ((region)::text = 'Jeju'::text)) ║
╚══════════════════════════════════════════════════════════════════════════════════╝
범위(Range) 조건의 쿼리
범위 단일 조건
25세 이하의 직원 정보를 조회하는 쿼리를 살펴보자. 이 쿼리는 <= 연산자가 사용되었기 때문에 순서 비교가 필요한 범위 조건의 쿼리이다. 이것 또한 간단하게 선택도를 계산할 수 있다. 25 이하에 포함되는 most_common_freqs 값을 전부 합산한 결과가 선택도가 된다. 0.0252 + 0.0242 + 0.0236 + 0.0241 + 0.0242 + 0.0258 = 0.1471 이므로, 선택도는 1.47%이다. 10,000행의 1.47%는 1,471행이므로, 옵티마이저의 실행 계획과 일치하는 것을 확인할 수 있다.
SELECT * FROM employee WHERE age <= 25;
most_common_vals | {20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34...
most_common_freqs | [0.0252, 0.0242, 0.0236, 0.0241, 0.0242, 0.0258, 0.0247, 0.0223, 0.0291, 0.0222, 0.0239, 0.024, 0.0273, 0.0231, 0.0247...
╔══════════════════════════════════════════════════════════════╗
║ QUERY PLAN ║
╠══════════════════════════════════════════════════════════════╣
║ Seq Scan on employee (cost=0.00..264.00 rows=1471 width=66) ║
║ Filter: (age <= 25) ║
╚══════════════════════════════════════════════════════════════╝
범위 복합 조건
BETWEEN(<=, >=) 조건도 마찬가지이다. 26세 이상, 30세 이하 조건에 해당하는 쿼리도 해당 범위에 포함되는 most_common_freqs 값을 합산해주면 된다. 0.0247 + 0.0223 + 0.0291 + 0.0222 + 0.0239 = 0.1222 이므로, 선택도는 1.22%이다. 10,000행의 1.22%는 1,222행이므로, 옵티마이저의 실행 계획과 일치하는 것을 확인할 수 있다.
SELECT * FROM employee WHERE age BETWEEN 26 AND 30;
most_common_vals | {20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34...
most_common_freqs | [0.0252, 0.0242, 0.0236, 0.0241, 0.0242, 0.0258, 0.0247, 0.0223, 0.0291, 0.0222, 0.0239, 0.024, 0.0273, 0.0231, 0.0247...
╔══════════════════════════════════════════════════════════════╗
║ QUERY PLAN ║
╠══════════════════════════════════════════════════════════════╣
║ Seq Scan on employee (cost=0.00..289.00 rows=1222 width=66) ║
║ Filter: ((age >= 26) AND (age <= 30)) ║
╚══════════════════════════════════════════════════════════════╝
히스토그램이 존재하는 범위 조건의 쿼리
사전 지식
필드에 히스토그램이 생성되어 있는 경우에는 계산 과정이 살짝 복잡해진다. salary 필드는 다음과 같이 MCF(most_common_freqs)와 histogram_bounds 값을 둘 다 가지고 있기 때문에 앞선 방식들처럼 단순하게 계산되지 않는다.
* 히스토그램 생성을 위해 employee 테이블을 초기화하고, 100만건의 데이터를 삽입하였다.
SELECT * FROM pg_stats WHERE tablename = 'employee' AND attname = 'salary';
-[ RECORD 1 ]-------------------------
schemaname | public
tablename | employee
attname | salary
inherited | False
null_frac | 0.0
avg_width | 4
n_distinct | 4993.0
most_common_vals | {6685,6711,6582,6571,6651,6769,6621,6730, ... (omitted)
most_common_freqs | [0.0011, 0.0010333334, 0.0009, 0.00086666667, ... (omitted)
histogram_bounds | {2001,2230,2334,2412,2479,2539,2596,2643,2701, ... (omitted)
correlation | 0.0027052828
most_common_elems | <null>
most_common_elem_freqs | <null>
elem_count_histogram | <null>
range_length_histogram | <null>
range_empty_frac | <null>
range_bounds_histogram | <null>
히스토그램은 MCV(Most Common Values)에 포함되지 않는 값들 중, 고유값이 2개 이상인 경우(최소 1개 이상의 구간)에만 생성된다. 따라서 전체 선택도(selectivity)를 1이라고 가정하면, MCV를 제외한 나머지 값들이 차지하는 비율은 히스토그램이 적용되는 데이터의 전체 비율로 볼 수 있다. 이 비율을 계산식으로 표현하면 (1 – MCV Selectivity) 이다.
*정확히는 NULL이 아닌 경우도 고려하여, (1 – nullfrac – MCV Selectivity)가 되어야 하나, 간결함을 위해 NULL이 아닌 경우는 제외하였다.
이 계산식은 실제로 아래와 같이 구현되어 있다. (selfunc.c)
- selec = 1.0 – stats->stanullfrac – sumcommon
– stats->stanullfrac: NULL의 비율
– sumcommon: MCV 선택도의 전체 합산 결과
– selec: NULL도 아니고, MCV도 아닌 값의 비율
히스토그램이 적용되는 데이터의 전체 비율(selec)을 구하면, 이제 이 값은 히스토그램 대상 비율이 된다. 그리고 여기에 히스토그램 내에서 조건(ex: salary BETWEEN 5000 AND 6000)을 만족하는 비율을 곱해주면, 히스토그램 대상 중 조건을 만족하는 비율이된다. 즉 히스토그램 선택도(hist_selec)가 계산된다.
- selec *= hist_selec
– hist_selec: 히스토그램 내에서 조건을 만족하는 비율
– selec: 히스토그램 대상 비율
마지막으로 대상 필드에 MCV가 존재한다면 히스토그램 선택도에서 MCV 선택도를 합산하여 최종적으로 쿼리 조건에 대한 선택도를 계산할 수 있다.
- selec += mcv_selec
– mcv_selec: MCV 선택도
– selec: 히스토그램 선택도
예시 쿼리
아래 쿼리를 가지고 계산 과정을 좀 더 자세히 살펴보도록 하자.
SELECT * FROM employee WHERE region = 'Seoul' AND salary BETWEEN 6750 AND 6800;
region = ‘Seoul’ 조건의 선택도는 동등 조건에서 살펴봤듯이 most_common_freqs 값이 선택도가 된다. ‘Seoul’ MCV에 해당하는 MCF는 0.14213334이므로, region = ‘Seoul’ 조건의 선택도는 14.2%이다.
most_common_vals | {Daejeon,Gwangju,Daegu,Busan,Jeju,Seoul,Gyeonggi}
most_common_freqs | [0.1445, 0.1443, 0.14346667, 0.1432, 0.14303334, 0.14213334, 0.13936667]
두 번째 조건의 salary 필드는 MCV와 Histogram이 모두 존재하기 때문에, 먼저 히스토그램이 적용되는 데이터의 전체 비율을 계산해야 한다. MCV Selectivity에 해당하는 sumcommon 값이 0.070233333이므로,
> SELECT sum(x) AS sumcommon
FROM pg_stats, unnest(most_common_freqs) as x
WHERE tablename = 'employee'
AND attname = 'salary';
+-------------+
| sumcommon |
|-------------|
| 0.070233333 |
+-------------+
히스토그램이 적용되는 데이터의 전체 비율은 0.929766666842624545 이다. 참고로 most_common_vals 필드에는 기본적으로 최대 100개(=default_statistics_target)의 MCV 값을 저장할 수 있는데, 100개 모두 저장되어 있다면 100번의 반복문을 돌면서 쿼리 조건(salary >= 6750)에 해당하는 MCV 선택도(mcv_selec)와, 100개 전체의 선택도(sumcommon)를 계산한다.
selec = 1.0 - stats->stanullfrac - sumcommon;
selec = 1.0 - 0 - 0.070233333157375455;
selec = 0.929766666842624545
다음으로는 히스토그램 내에서 조건을 만족하는 비율인 hist_selec을 계산해야 한다. histogram_bounds 필드는 기본적으로 최대 101개의 경계값을 저장할 수 있다. 왜냐하면 default_statistics_target + 1의 경계값을 저장해야 100개의 히스토그램 구간이 생성되기 때문이다. MCV 선택도를 계산할 때와 마찬가지로 100+1개의 히스토그램 경계값 루프를 통해 실제 쿼리 조건(salary >= 6750)에 해당하는 구간을 찾되, 이진 탐색(Binary Search)으로 좀 더 빠르게 조건 값이 속하는 구간을 찾는다.
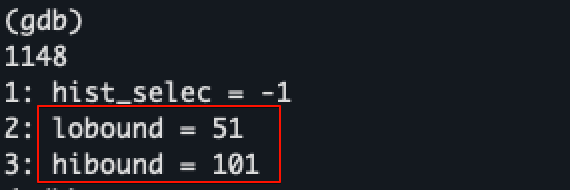
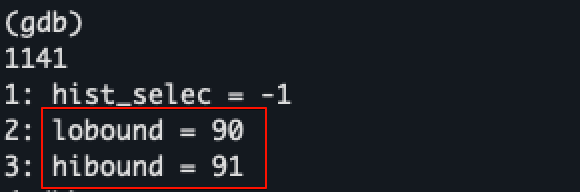
쿼리 조건에 맞는 히스토그램 구간(=91)을 찾으면, 구간 내에서도 조건 값이 어느 위치에 있는지 파악해야 정확하므로, 다시 구간 내 상대적 위치(binfrac)를 계산한다. 예를 들어 91번째 구간의 중간 지점에 6750 값이 존재한다면, 0.5만큼을 더 포함시키는 것이다.
추가로, 누적 비율(hist_frac)이라는 것도 계산하는데, 이것은 조건 값보다 작은 모든 구간 + 현재 구간(=91) 내에서의 데이터 비율을 파악하기 위함이다. 계산 과정이 어렵지는 않기 때문에 상세 내용은 ineq_histogram_selectivity() 함수를 참고하면 된다.
위 과정을 통해 히스토그램의 선택도(hist_selec)까지 계산하고 나면, salary >= 6750 조건의 선택도를 계산하기 위한 모든 단서들을 얻게 된다.
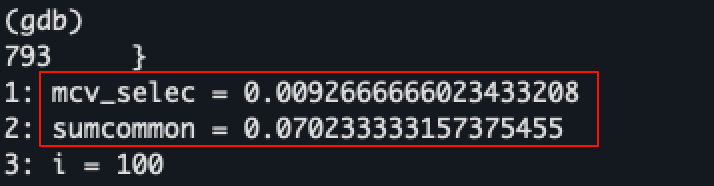
따라서 아래 산식에 의해 선택도는 0.10140027896848625가 된다.
- mcv_selec: 0.0092666666023433208
- stats->stanullfrac: 0
- sumcommon: 0.070233333157375455
- hist_selec: 0.099093262483820332
# salary >= 6750의 선택도 계산 과정
selec = 1.0 - stats->stanullfrac - sumcommon = 1.0 - 0 - 0.070233333157375455
selec *= hist_selec = 0.092133612366142924239647789113248940
selec += mcv_selec = 0.101400278968486245039647789113248940
--> 0.10140027896848625
나머지 조건 salary <= 6800의 선택도 또한 계산 과정을 통해 0.92520915151806549로 계산된다.
이제 마지막 과정이 하나 남아있다. 사실 지금까지의 salary 필드에 대한 선택도 계산은 그림 3과 같이 계산되었다. 즉 교집합을 제외한 나머지 영역은 각 조건에 위배되는 영역이기 때문에 그림 4와 같이 공통 영역만을 고려해서 선택도를 다시 계산해야 한다는 의미이다.
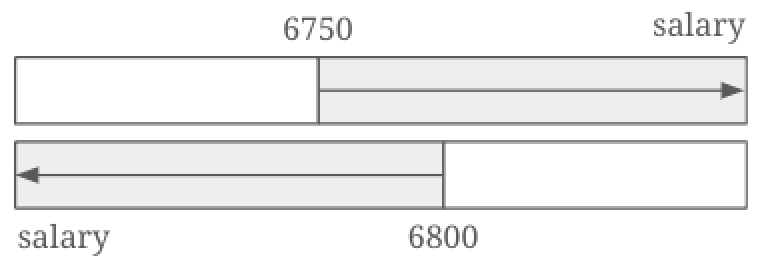

계산 방법은 간단하다. 확률의 교집합 공식을 사용하면 된다.
- P(A ∩ B) = P(A) + P(B) − P(A ∪ B)
- P(A) = 0.10140027896848625
- P(B) = 0.92520915151806549
- P(A ∪ B) = 1.0
- P(A ∩ B) = 0.10140027896848625 + 0.92520915151806549 – 1.0 = 0.02660943048655174
위 계산 과정에 따라 salary BETWEEN 6750 AND 6800 조건을 만족하는 최종 선택도는 0.02660943048655174가 된다. 그리고 너무 일찍 계산해서 잊어버렸을지도 모르지만 region=’Seoul’ 조건의 선택도 0.14213334까지 논리곱으로 계산하면 전체 쿼리 조건 region=’Seoul’ AND salary BETWEEN 6750 AND 6800에 대한 선택도는 0.14213334 ✕ 0.02660943048655174 = 0.0037820872305514238890116으로, 0.3782%가 된다.
1,000,000행의 0.3782%는 3782행이므로, 옵티마이저의 실행 계획과 일치하는 것을 확인할 수 있다.
EXPLAIN SELECT * FROM employee WHERE region = 'Seoul' AND salary BETWEEN 6750 AND 6800;
╔══════════════════════════════════════════════════════════════════════════════════════════════╗
║ QUERY PLAN ║
╠══════════════════════════════════════════════════════════════════════════════════════════════╣
║ Gather (cost=1000.00..17177.87 rows=3782 width=36) ║
║ Workers Planned: 2 ║
║ -> Parallel Seq Scan on employee (cost=0.00..15799.67 rows=1576 width=36) ║
║ Filter: ((salary >= 6750) AND (salary <= 6800) AND ((region)::text = 'Seoul'::text)) ║
╚══════════════════════════════════════════════════════════════════════════════════════════════╝
참조
- Database System Concepts 6th – Estimating Statistics of Expression Results
- https://www.postgresql.org/docs/current/row-estimation-examples.html
- https://www.postgresql.org/docs/current/multivariate-statistics-examples.html
- https://github.com/postgres/postgres/blob/master/src/backend/commands/analyze.c
- https://github.com/postgres/postgres/blob/master/src/backend/utils/adt/selfuncs.c
- https://github.com/postgres/postgres/blob/master/src/backend/optimizer/path/clausesel.c
- https://github.com/postgres/postgres/blob/master/src/backend/optimizer/path/costsize.c

댓글 남기기